Before venturing into the subject matter of this treatise, a few definitions are required. The two mutually antagonistic concepts which are at the core of the present discussion are order and chaos. Reginald Firehammer, who mistakenly seeks to demonstrate that the universe is characterized by a fundamental disorder, writes in his essay, “Disorder, Chaos, and Existence,” that the term, “order” tends to have two widespread interpretations:

The two most common meanings are related: there is order in the sense of being, "lined up," or "organized," according to some priority or hierarchy; and there is order in the sense of uniformity or regularity. The important difference is that things can be orderly in the first sense (organized) and totally disorderly in the second sense (uniformity), and in fact, things organized in the first sense cannot be truly orderly in the second.

            This distinction is an accurate one, and necessary to identify precisely what the proponents of reason consider to be an “orderly universe.” An orderly universe is not one which displays perfect uniformity or regularity; such a universe would need to be homogeneous, and, from simple empirical observation of the world around us, we know this to be false. All macroscopic entities are heterogeneous, composed of a variety of elements and structural arrangements thereof. Furthermore, entities are separated from each other spatially, and, in the region of their separation, no entities exist. Had the universe truly been uniform and homogeneous, it would have consisted of one giant entity with absolutely constant texture and composition throughout, stretching for infinity in all three spatial directions, itself an inconceivable scenario.

            Instead, an orderly universe is one which is “organized” according to premises that can be known and fathomed by the human mind. This organization was not imposed upon the universe by any external “higher” entity, unless that higher entity is man with his capacity to rearrange the elements into even more orderly combinations. On the contrary, the organization is inherent in the natures of entities themselves. Every entity is what it is. By implication, it has a specific identity which describes what it is. Its identity is a sum of finite, measurable qualities which is distinct from the entire set of measurements for any other entity, but is related to the qualities of every other entity in some way (be it a certain distance of spatial separation, temporal separation, or a specific process or active relationship occurring among different entities).

            If every entity has a finite, measurable identity, and these finite, measurable identities must be mutually related in some way, then it follows that this sum of identities and relationships constitutes the organization which defines an orderly universe. By the study of the entities’ identities and relationships, it is possible to discern the underlying order for any given entity, quality, or relationship. There is no entity which is not orderly in a fundamental way, whatever the specific premise behind its organization might be, for the organization itself is what makes it possible for us to understand the entity’s nature. If an entity lacks any sort of order, it cannot possibly be understood by man—man would not even know that such an entity could exist. How could he have this knowledge if that entity had no clear, definite, organized manner by which to manifest its presence?

            Human reason is defined as the ability to non-contradictorily identify elements of reality. If an entity is unfathomable by means of reason, it cannot be non-contradictorily identified. If it cannot be non-contradictorily identified, then there must be a fundamental contradiction in the very assumption that the entity exists. Any such contradiction can only be resolved by asserting that such an entity does not, in fact, exist. Therefore, anything which cannot be fathomed by human reason also cannot exist. Thus, in order to exist, any entity must have some sort of fathomable underlying order to it.

            Since we defined order as fathomable organization, we shall now define chaos as the absence of order, i.e., the lack of fathomable organization. Since we have just demonstrated that anything without such an organization cannot possibly exist, it shall be the guiding premise of our further exploration that indeed, chaotic entities and fenomena cannot exist in the universe.

The Misnamed Theory

            “Chaos theory” is a branch of mathematics dealing with systems and fenomena which might defy one’s original expectation of what orderly entities, qualities, and relationships consist of. David Harrison of the University of Toronto Department of Physics writes:

“When people began to study the systems we discuss below, they seemed utterly disorganized. Thus they were called "chaotic." As work progressed we discovered that hidden in the apparent disorganization was a great deal of structure. The structure shared by all of these systems then became the technical definition of these systems, which we continue to call "chaotic." So the technical meaning of chaos now means something quite different from the everyday meaning.”

            We can thus understand that the name “chaos theory” did not stem from the fact that the existents it studied were truly chaotic, in the sense of not having any underlying order or structure. In fact, despite the seeming disorganization upon first impression, there is indeed a vast amount of order in systems known as “chaotic” in the technical sense of the word. Indeed, the fenomena were first named as being chaotic, and then discovered, through closer examination, to be orderly on a fundamental level. The name for the systems and the theory describing them was not born of factual observation, but of hasty beforehand assumptions which were later refuted by deeper study.

            Unfortunately, the name remained despite the known fact that the existents it described did not in fact exhibit true chaos. While the scientists and mathematicians themselves can get away with using such a name in their own realm of work by simply assigning a different meaning to it, such an approach creates immense confusion and harm in the public perception of science, mathematics, and the question of whether the universe is orderly.

However mathematicians might redefine “chaotic systems” to mean systems exhibiting a specific set of known, fathomable properties, the conventional definition of chaos, and, more importantly, the filosofical definition of chaos, is that of the absence of organization and structure. Thus, while mathematicians are in fact describing systems which are perfectly organized and fathomable in their own way, the rest of the world will interpret them as stating that “there are some things which cannot be known, because they lack any fundamental order.” The popular perception of chaos theory is that of a “proof” that there are some absolutely random aspects to the universe which no individual can ever possibly know in full. It is true that the very notion of mathematics “proving” the inapplicability of order (on which mathematics itself is based) to some part of reality is a logical contradiction, but who would care about logical contradictions if it were thought that some aspects of the universe were off limits to logic? 

It is therefore time for the name “chaos theory” to be changed. This name was coined due to assumptions which did not hold true; it contradicts the body of the theory it describes, and it fosters an improper perception of the universe in the eyes of the public, and, in particular, the non-scientifically-specialized intellectuals. The name, “Theory of Subtle Order” might be a better indicator of the nature of the fenomena which are the province of said theory’s study. The order within a given class of fenomena might indeed not be apparent to the untrained observer at first glance, but this does not mean that the order itself does not exist. It is simply more subtle and complex than the typical forms of organization. To state that whatever order one’s first hunch is not capable of discerning is not in fact order, but rather “chaos,” is a type of hubris which presumes, in essence, that “if I cannot see it right away, it must not be there at all.”

The remainder of this treatise shall be devoted to several brief explorations of how the basic systems studied by the theory under present discussion are in fact remarkably orderly in their own way. 

Fractal Sets 

Reginald Firehammer writes:

“Fractals are called "iterative," which only means, a particular equation is repeated over and over. In fractal math, the "output" of each iteration of an equation, is used as one of the variables of the equation for the next iteration.”

            A common fractal equation for the Julia and Mandelbrot sets is the recursive expression x’=x²+c. That is, the subsequent term in the sequence is the square of the previous term plus some constant “c.” Depending on choices for initial values of x and c, the sequence produced will be different. Where Mr. Firehammer errs, however, is in presuming that such a system somehow exhibits an inherent disorder of any sort. He writes:

“Two aspects of fractals are already apparent, however, no number ever repeats, and the results cannot be predicted, except in this case it can be predicted the numbers keep getting bigger.”

            It is true that no number ever repeats in a fractal sequence, but it is unwarranted to assume that this is a mark of disorder. In fact, the simple recursive sequence, x’=x+1, in which the subsequent term is the previous term plus one, would never repeat a single term, yet to claim that a specific example of such a  sequence, “1, 2, 3, 4, 5, 6, 7, etc.,” is disorderly is surely false.

            Furthermore, although the initial algorithm for a fractal sequence can only be defined recursively, this does not mean that the results are unpredictable. It only takes a different way of looking at the expression for the Julia set to see the underlying pattern, which can be extrapolated as many times as one sees fit.

            Let us presume that we are starting with some initial value, X_0, and some given constant, c. The algorithm which we apply to every subsequent term is, again, x’=x²+c. What results is the following:

 

X₀=X₀

X₁=X₀²+c

X₂=(X₀²+c)²+c

X₃=((X₀²+c)²+c) ²+c

X₄=(((X₀²+c)²+c) ²+c) ²+c

 

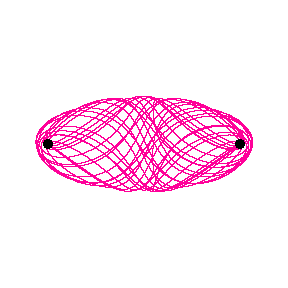
What beauty, what order, what elegance! The number of c's in the expression matches precisely the subscript of the x, and there is precisely one X₀ term needed in every explicit formula for every term. As a matter of fact, one would be able to obtain the explicit formula for X₁₀₀₀ just by extrapolating the pattern above, though it would take one quite a long time to write it. Computers, of course, can produce and process such formulas in an instant. Furthermore, one could easily write out the formula for X₁₀₀₀ without ever bothering to determine X ₉₉₉ or any of those intermediate values in the sequence. One only needs to know how many parentheses and how many “c” values to include in the expression. (In this case, the minimum number of parentheses needed is one less than the number of the subscript of X, and the pattern of the parentheses’ recurrence is constant and unchanging.) Any nth iteration of this algorithm is perfectly predictable, provided that one knows the initial term X₀, the value of c, and the value of n (the number of iterations). Then, one can write out the explicit formula for X_n, in terms of X₀ and c, fill in the precise numerical values for X₀ and c, and thereby get a numerical output.

Let us examine another fractal set which Mr. Firehammer seeks to use to demonstrate the “disorderliness” of such sets. Mr. Firehammer writes:

“A better example is (x-c)/x = x' [x=1, c=3, x` is the value of x for the next iteration]

The first iteration is therefore: (1-3)/1 = x', or -2/1= -2. The series begins as follows:

-2/1 = -2
-5/-2 = 2.5
-.5/2.5 = -.2
-3.2/-.2 = 16
13/16 = .8125
-2.1875/.8125 = -2.692307
-.307692/2.692307 = -.114285
-3.114285/-.114285 = .355918
3.355918/.355918 = 9.428899
6.428899/9.428899 = .681829
-2.318170/.681829 = -3.399928

The output of all equations produces a series of values: -2, 2.5, -.2, 16, .8125, -2.692307, -.114285, .355918, 9.428899, .681829, -3.399928, .... (All values have been truncated to 6 decimal places.) The series is indefinite and never repeats. Notice that the change in signs seems to be random. It is not random, because it is determined by the equation and input values, but cannot be predicted. In fact, no part of the series can be predicted.”

            When one just visually examines the numbers, one is certainly intimidated at first glance. “What possible order can there be here?” one might ask. But the order is there, just waiting to be grasped. It is merely hiding behind an extremely thin veneer of apparent randomness. In fact, this algorithm is just as predictable as the Julia set. Let us examine the lineup of explicit formulas for it:

X₀=X₀

X₁= (X₀-c)/ X₀

X₂=((X₀-c)/ X₀-c)/ X₀

X₃=(((X₀-c)/ X₀-c)/ X₀-c)/ X₀

X₄=((((X₀-c)/ X₀-c)/ X₀-c)/ X₀-c)/ X₀

                There is a beautiful order here, once again. It is found in a pattern using which the explicit formula for any term in the sequence can be easily determined. Here, the minimum number of parentheses equals the subscript of the X, as does the number of X₀ terms in the expression. The number of “c” terms in the expression is one less than the subscript of the X, and the pattern by which parts of any given explicit formula recur is constant. By writing out the explicit formula for any X_n, it becomes possible to predict the value of X_n without necessarily working out all the terms prior to it.

It is true that fractal sequences like the Julia and Mandelbrot set can only be known through an initial recursive formula, but this by no means implies that they are disorderly or unpredictable. Let the reader examine the following string of numbers:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, etc.

If the reader just looks at the numbers, the pattern does not display itself automatically. Is it thereby random or “chaotic”? By no means. As a matter of fact, this sequence, like the fractal sets, can only be known through a recursive formula. In this case, the recursive formula is X_n+1= X_n+ X_n-1. By the way, I have just given the reader the means to uncovering the underlying order of this sequence: each subsequent term is the sum of the previous two terms.

This, of course, is the famous Fibonacci Sequence. A curious thing happens to the ratios of each subsequent term over the term preceding it as the sequence continues indefinitely. These ratios approach an asymptote: the “transcendental” number 1.61803…, otherwise known as φ, or the Golden Ratio. From the time of the ancient Greeks onward, the Golden Ratio was thought to be the proportion representative of the ultimate beauty and the ultimate orderliness of the universe. And this portrayal of ultimate beauty and order can only be accessed through an initial recursive formula! Seeing this, can the proponents of the view that the universe is “chaotic” any longer accurately claim that fractal sets are indicative of universal disorder simply because they are recursive?

Quite the contrary, recursivity automatically implies an underlying order in a sequence which exhibits it. Recursivity entails the requirement of repeated iteration of the same function, and this repetition in iteration is in itself a pattern which can be shown more explicitly as well. One will be able to perform the same demonstration as I had done to show the underlying order of the two fractal sets above with any recursive sequence, fractal or not.

The Three-Body Problem

Another example of a system which is commonly called “chaotic” is the hypothetical case of a planet rotating about two “suns.”  The path of such a planet is complicated and does not repeat itself, unlike the fairly elementary elliptical path of a planet in orbit around a single sun. Because the path never repeats itself, it is assumed that, if it should continue indefinitely, we should get ever new trajectories for the planet to follow, which would thereby make its motion unpredictable and disorderly. This assumption is mistaken on several counts, however.

First, no matter how many entities are involved in a gravitational interaction, any two of them will follow Newton’s Law of Universal Gravitation with respect to one another. That law is expressed as F= Gm₁m₂/r²,  where F is the force of gravity on either body, G is the universal gravitational constant, r is the distance between the centers of the two bodies, and the subscripted m terms are the mass values for each respective body. Any gravitational interaction, no matter how complex, is just a finite set of interactions, each of which follows the principle of F= Gm₁m₂/r², an underlying principle for the system. If each gravitational interaction which is a member of the set can be known through the above universal law, then it follows that all members of the set can be thus known. In practice, the calculations required to achieve this knowledge might be numerous and time-consuming, but they are capable of being performed, as any underlying order such as this is capable of being explicated. Computers can speed up the process considerably, as the very “chaos” mathematicians themselves have discovered.

Second, it is a mistake to assume that real three-body systems would exhibit paths of motion which continue on indefinitely. Consider the following output of a computer model of a three-body interaction which has only been performed for eighty iterations (courtesy of David M. Harrison’s “An Introduction to Chaos”):

 

Let the reader note how dangerously close the planet would be getting to both of the suns so many times during only the first eighty time units of its rotation!  The mistaken assumption this particular model makes is that of the point-like natures of the “suns” and the planet involved. The point model is a customary simplification for fysical simulations, but in this case it presents a potentially grave misapplication of the three-body problem to reality. Real entities are always three-dimensional, and real planets are always three-dimensional sferes or sferoids. Simply put, if two sferoids were to get as close to each other as the above diagram suggests, they would collide into one another, and the motion along the path predicted above would stop! As a matter of fact, because temperatures of a given sun are likely to be colossal, the planet will be consumed and melted by the sun, and the three-body system would cease to exist. Thus, any path the planet would take would occur only over a finite, and likely rather small, number of time intervals. This implies that determining such a real-world path prior to collision would take a finite amount of applications of Newton’s Law of Gravitation, which a computer would be able to do even if a human being could not. The finite path thus determined might curve every which way, but it would still be knowable via a definite algorithm and would thus be orderly in a fundamental sense.

            In response to this reasoning, Mr. Firehammer wrote on the Autonomist Forum: “The closest scientists have been able to come to solving the three-body problem is by assuming the bodies are single points in a single plane. Real bodies obviously are not points. Since they cannot even solve the problem for this model which reduces all aspects of the problem to simplest terms, it is obvious they cannot solve the problem for real bodies.” Mr. Firehammer’s assumption is that a point model is necessarily simpler and easier to operate on than a model which incorporates the three-dimensional nature of entities. However, this assumption is false for cases such as this. The point model is in fact more laborious to apply here than the three-dimensional model, because the point model rules out the possibility of collisions between the planet and one of its suns, and would thus require one to continue extrapolating an indefinite, ever-different trajectory. Reductionism can often result in more work and more difficulty in arriving at an answer than an approach which does not rule out any known data, allegedly for convenience’s sake.

            My answer as to the orderliness of any trajectory of motion determined by three-body gravitational attraction is evident in reality itself. In fact, we observe that there are no known actual situations where a given planet revolves around two suns; such solar systems are but the stuff of science fiction. We know why this is the case: any three-body trajectory is going to inevitably (and rather soon) result in a collision between two of the bodies. Even if there had been any three-body systems in the universe’s history, they would have quickly become obliterated. The only solar systems that remained were those with a single sun, which could facilitate the rotation of planets about it in simple, repeating, elliptical orbits. The more stable and orderly a given system, the more reality favors it, and the more it is naturally selected over less stable and less orderly systems.

            Because collisions in any three-body gravitationally-originated motion are inevitable, we conclude that all three-body problems result in finite trajectories which can be relatively easily, for our technological level, understood and modeled via a guiding principle, Newton’s Law of Universal Gravitation.

            Characteristics of “Chaotic” Systems

       Ample additional evidence can be found, demonstrating that the systems mathematicians and scientists refer to as “chaotic” in the technical sense are in fact quite orderly. Dr. Harrison provides a full description for the layman of some of the basic attributes and underlying principles of organization which are said to characterize “chaotic” systems. Here, I shall simply provide a summary citation so as to give an idea of the types of evidence for the validity of my thesis which a deeper study of these systems will uncover. Such systems entail the following.

•  Sensitive Dependence on Initial Conditions.
• The trajectory never repeats.
• They are nonlinear.
• The transition to chaos is preceded by infinite levels of bifurcation.
• The infinite bifurcations preceding the transition to chaos are characterised by the Feigenbaum number.
• Fractional dimensionality.
• A Lyapunov plot of the distance between trajectories versus time will exhibit a straight line.
• The initial points of the first return map always lie above a line making an angle of 45 degrees with the horizontal.

“Thus, hidden in the apparent disorganization is a great deal of structure. [Harrison’s words, not mine, but further supporting my point.]”

            “Chaotic” systems are not chaotic at all, in the layman’s and the filosofical sense of the word. Chaos is the absence of structure, but these systems exhibit a plethora of organization.  Such systems are only a specific type of mathematical and fysical scenarios which are grouped together into their own branch of study because they share certain common, underlying properties. It is a worthwhile endeavor to study these systems and their properties, precisely because such study will uncover more underlying order behind them. This underlying order, aside from being understood, can be applied by man to manipulate entities in the absolute reality so as to best serve his own interests. It can be used, for example, for modeling short-term weather trends, or for discovering the structure of a fern plant, or for attaining an understanding, as I had demonstrated, of why planetary systems with two or more suns are impossible in the real universe.

“Chaos theory” remains, at its core, a branch of mathematics, and mathematics cannot be used to show its own inapplicability to reality. No system can, within its own premises, refute itself, unless it is self-contradictory, which mathematics is not. Mathematics is specifically defined and structured so as to exclude the possibility of contradiction, for mathematics is an outgrowth of logic, which Ayn Rand called “the art of non-contradictory identification.”

As a means of describing the orderliness of certain existents, “chaos theory” should be welcomed and explored further. However, it is in need of an urgent name change, for it is truly the “Theory of Subtle Order,” which supplements, not refutes, the rationally comprehensible nature of all of existence. There is no province of knowledge inherently off limits to man, for what cannot be known, cannot be. Let us not take our newly discovered key and use it as a justification for throwing away the hand of reason which must use it to unlock all the mysteries of the universe.

G. Stolyarov II is a science fiction novelist, independent filosofical essayist, poet, amateur mathematician and composer, contributor to organizations such as Le Quebecois Libre, Enter Stage Right, the Autonomist, and The Liberal Institute. Mr. Stolyarov is the Editor-in-Chief of The Rational Argumentator. He can be contacted at gennadystolyarovii@yahoo.com.